 |
Getting Started |  |
| Syntax & Backus-Naur Form |
| Main | |
|
|
Latest News |
|
|
Getting Started |
|
|
Screen Shots |
|
|
Download |
|
|
Documentation |
|
|
Contributors |
|
|
Contact |
| About GOLD | |
|
|
How It Works |
|
|
FAQ |
|
|
Why Use GOLD? |
|
|
Comparison |
|
|
Revision History |
|
|
Freeware License |
|
|
More ... |
![]()
Syntax
The term "syntax" refers to the structure of a programming language, in particular, the different series of symbols and words that make up the basic parts of the language. The most common way of specifying the syntax of a language is use a notation known as Backus-Naur Form.
Backus-Naur Form
Terminals & Nonterminals
Backus-Naur Form, BNF for short, is a notation used to describe grammars. The notation breaks down the grammar into a series of rules - which are used to describe how the languages lexical and syntactic structures are used to form different logical units
The actual reserved words, symbols, etc... of the grammar are represented "terminals". In Backus-Naur Form, terminals are usually left without any special formatting or are simply delimited by single or double quotes. Examples include: if, while, '=' and identifier.
Syntactic rules are represented with a "nonterminal" - which are structure names. Typically, nonterminals are delimited by angle-brackets, but this is not always the case. Examples include <statement> and <exp>. Both terminals and nonterminals are referred to generically as "symbols".
Productions
The actual syntax of the grammar is specified by combining terminals and nonterminals into syntactic rules known as "productions". They have the following format:
| N ::= s |
where N is a nonterminal and s is a series of zero or more terminals and nonterminals. Different alternatives can be specified in Backus-Naur Form. For readability, often productions are grouped together and separated by a “pipe” symbol - which is read as the word “or”.

Basically, a production has the following properties.
- The production starts with a single nonterminal, which is the name of the structure being defined
- This nonterminal is followed by a ::= symbol
which means “as defined as”. The ::= symbol
is often used interchangeably with the
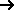 symbol. They both have the same meaning.
symbol. They both have the same meaning. - The symbol is followed by a series of terminals and nonterminals.
Note: In GOLD, groups of related productions are called "rules". This is nonstandard terminology.
Examples
For example, the following defines a rule called <Value> which can contain either an Identifier terminal or the contents of another rule called <Literal>
| <Value> ::= Identifier |
<Literal> <Literal> ::= Number | String |
The <Literal> rule can contain either a Number or String terminal. As a result of this definition, a <Value> can contain an Identifier, Number or String.
Rules can also be recursively defined. The following rule defines a series of one or more Identifiers.
| <Identifiers> ::=
<Identifiers> Identifier | Identifier |